Profunctor Optics a Categorical Update (Clarke, Elkins, Gibbons, Loregian, Milewski, Pillmore, Román)
Abstract Optics are bidirectional data accessors that capture data transformation patterns, such as accessing subfields or iterating over containers. Profunctor optics are a particular choice of representation supporting modularity, meaning we can construct accessors for complex structures by combining simpler ones. Profunctor optics have been studied only in an unenriched and non-mixed setting, in which both directions of access are modelled in the same category. However, functional programming languages are arguably better described by enriched categories; and we have found that some structures in the literature are mixed optics, with access directions modelled in different categories. Our work generalizes a classic result by Pastro and Street on Tambara theory and uses it to describe mixed V-enriched profunctor optics and to endow them with V-category structure. We provide some original families of optics and derivations, including an elementary one for traversals. Finally, we discuss a Haskell implementation: the vitrea library is a lightweight version of the original Kmett’s lens library that popularized optics to functional programmers.
“Profunctor Optics, a Categorical View” was recently published at Compositionality. It is the result of joint work during the 2018 Adjoint School, where Bartosz Milewski, Derek Elkins, and later Jeremy Gibbons mentored a group consisting of Bryce Clarke, Fosco Loregian, Emily Pillmore and me. We are thankful to the Adjoint School, and I would like to highlight it as a crucial piece of community-building around category theory applications.
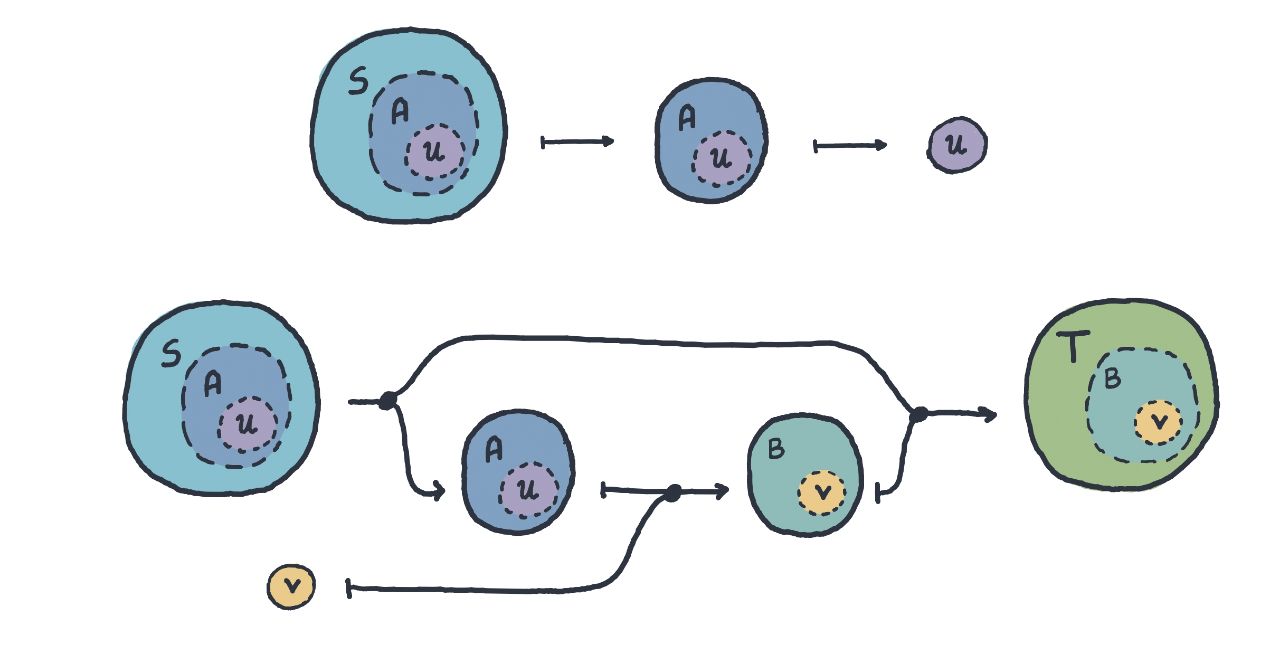Since we started the project, optics have become quite a popular topic, and they have found multiple disparate applications, all linked by the same core idea of bidirectional interaction. Without trying to be exhaustive:
Capucci, Gavranović, Hedges and Rischel are inspired by cybernetics;
Stein and Staton employ them for exact conditioning in probabilistic programming;
Smithe has proposed optics for active inference;
Cruttwell, Gavranović, Ghani, Wilson and Zanasi study gradient-based learning;
Cappuci and Videla study server architecture;
Atkey, Gavranović, Ghani, Kupke, Ledent, Forsberg and
Genovese, Loregian and Palombi use them for economic game theory;
Garcia de Oliveira, Jaskelioff, and Vieira de Melo motivate with optics the development of monoidal profunctors in functional programming; and
Nguyễn has a mention for optics while developing automata in linear logic. Iteration is the subject of at least two different approaches, one by
Hedges and Sakamoto and one developed in joint work with
Di Lavore and de Felice. The whole framework has been later extended by
Vertechi,
Milewski,
Capucci,
Braithwaite, Capucci, Gavranović, Hedges and Rischel, and in my joint work with
Braithwaite,
Hefford and
Earnshaw. I have also tried to complete this story linking optics to
“incomplete string diagrams” and
“quantum combs”.
Optics may be a useful addition to your toolbox; this paper tries to be both a unification of the previous theory on optics and a repository of tools and ideas to help the reader adapt the optics framework to their particular application.