Promonads and String Diagrams for Effectful Categories (Román, 2022)

Last updated Jan 9, 2025

Alan Jeffrey (in 1997) articulated a string diagrammatic syntax for the semantics of imperative pro- gramming: an extra wire was employed for global effects. I promoted Jeffrey’s techique into a freeness, soundness and completeness proof of a graphical calculus of premonoidal and effectful categories. In the same way that monoidal categories are pseudomonoids in the bicategory of categories, my effectful cate- gories are pseudomonoids in a monoidal bicategory of promonads.

Effectful program in string diagrammatic notation and arrow-do notation.

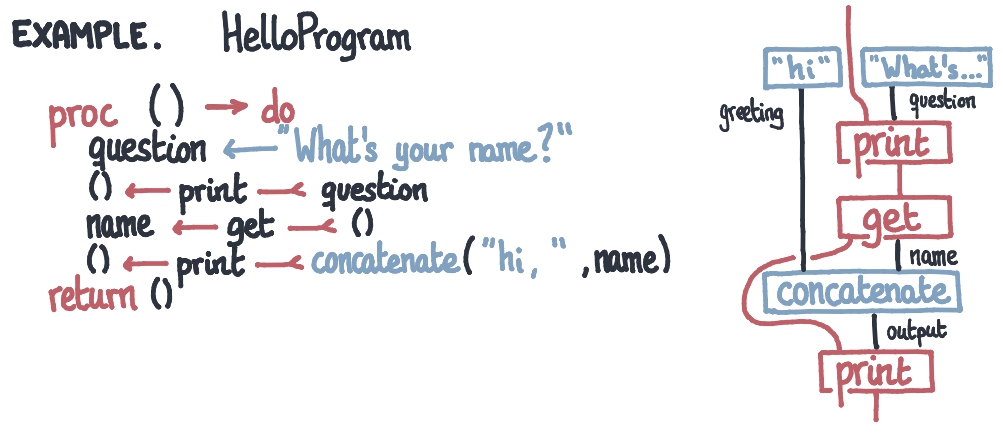Abstract. Premonoidal and Freyd categories are both generalized by non-cartesian Freyd categories: effectful categories. We construct string diagrams for effectful categories in terms of the string diagrams for a monoidal category with a freely added object. We show that effectful categories are pseudomonoids in a monoidal bicategory of promonads with a suitable tensor product.

# How to cite

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
@inproceedings{effectful22,
  author       = {Mario Rom{\'{a}}n},
  editor       = {Jade Master and
                  Martha Lewis},
  title        = {Promonads and String Diagrams for Effectful Categories},
  booktitle    = {Proceedings Fifth International Conference on Applied Category Theory,
                  {ACT} 2022, Glasgow, United Kingdom, 18-22 July 2022},
  series       = {{EPTCS}},
  volume       = {380},
  pages        = {344--361},
  year         = {2022},
  doi          = {10.4204/EPTCS.380.20},
  timestamp    = {Fri, 11 Aug 2023 14:29:27 +0200},
}

Related

References