Promonoidal category of optics

Last updated Apr 23, 2024

See also

• Doubles for Monoidal Categories (Pastro and Street, 2008)
• Open Diagrams via Coend Calculus (Román, 2020)
• optics
• Monoidal contexts

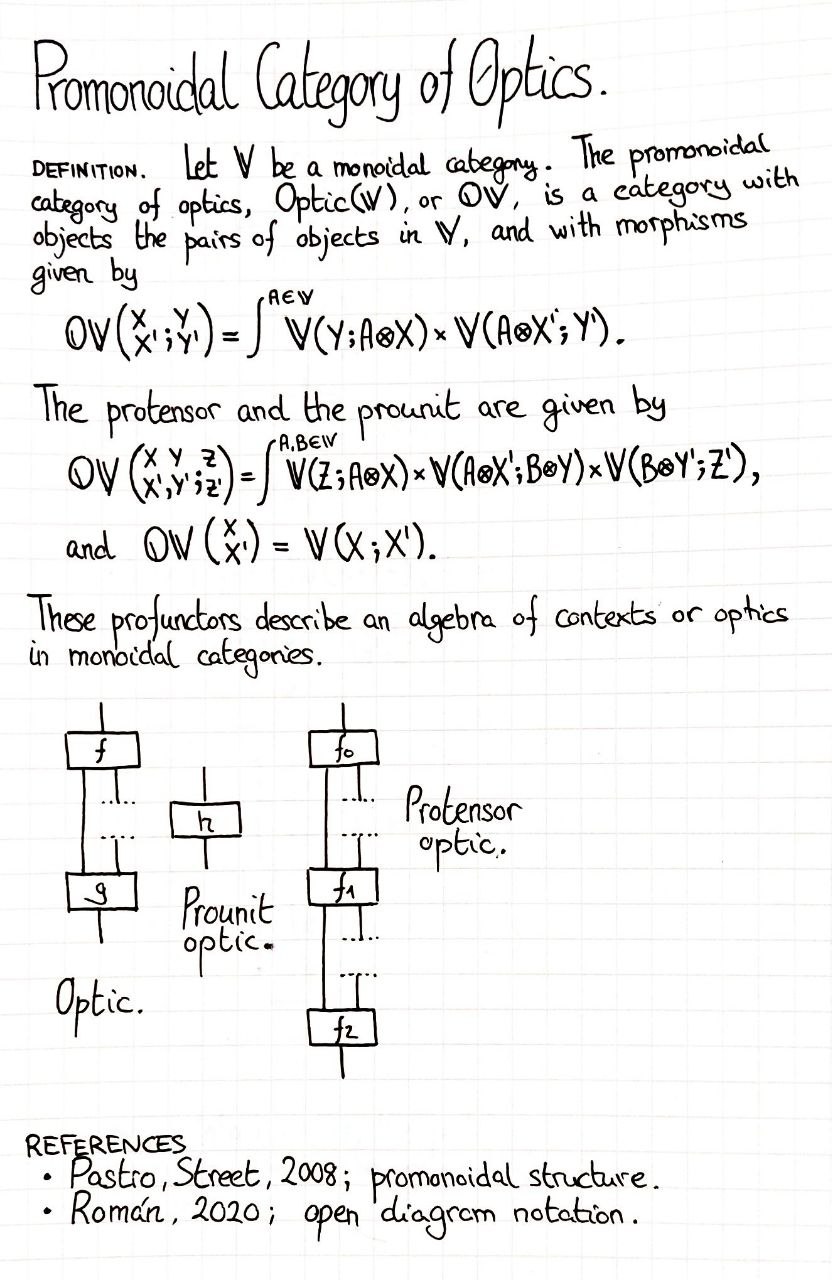
Let $𝕍$ be a monoidal category. The promonoidal category of optics $\operatorname{Optic}(𝕍)$ is a category with the same objects as $𝕍 × 𝕍^{op}$ and with morphisms given by $$ \operatorname{Optic}(𝕍)\left( \binom{X}{X’};\binom{Y}{Y’} \right) = ∫^{A \in 𝕍} 𝕍(Y; A ⊗ X) × 𝕍(A ⊗ X’; Y’). $$ The promonoidal structure is given by $$ \operatorname{Optic}(𝕍)\left( \binom{X}{X’},\binom{Y}{Y’};\binom{Z}{Z’} \right) = ∫^{A \in 𝕍} 𝕍(Z; X ⊗ A) × 𝕍(A ⊗ X; B ⊗ Y) × 𝕍(Y ⊗ B’ ; Z’), $$ $$ \operatorname{Optic}(𝕍)\left( \binom{X}{X’} \right) = 𝕍(X,X’).$$

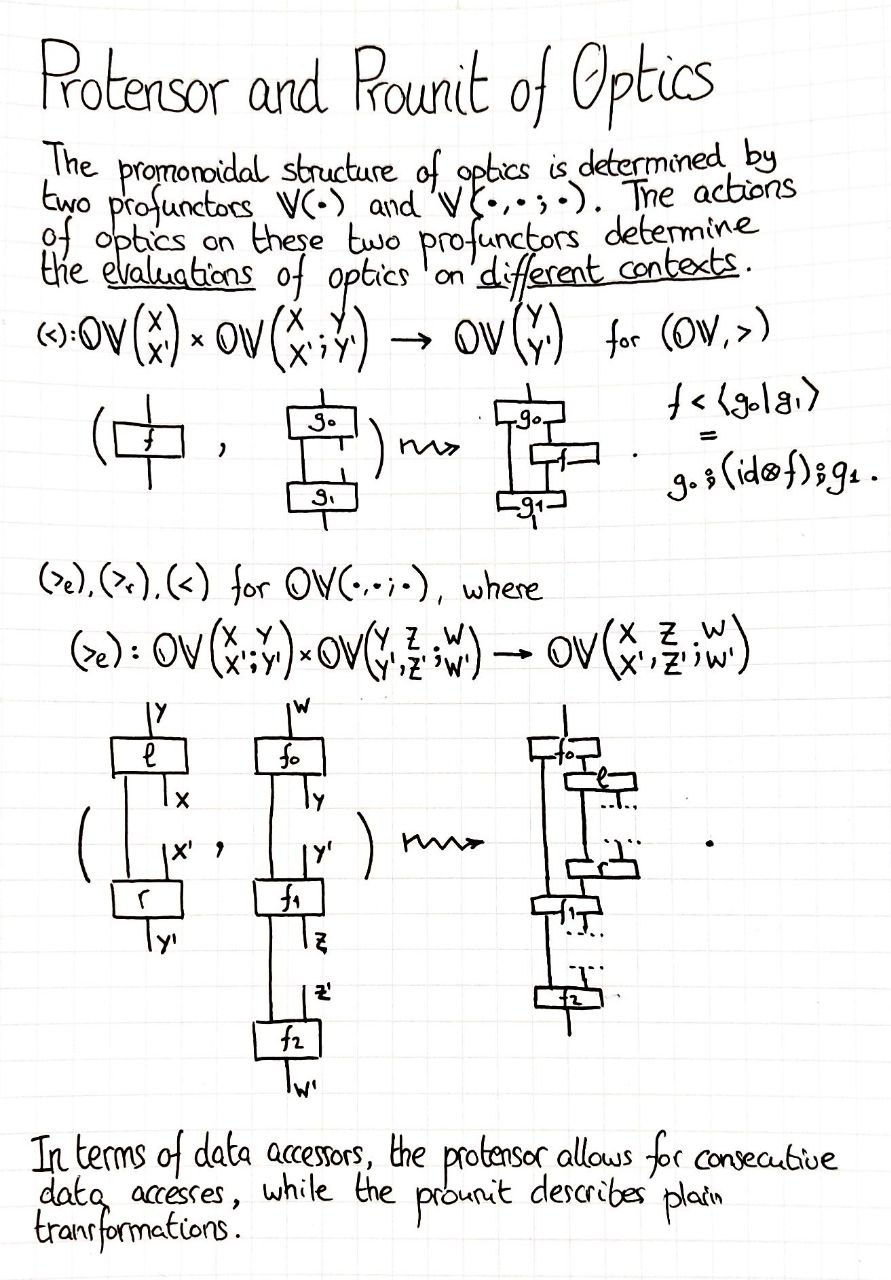
The promonoidal structure of optics is determined by two profunctors $𝕆𝕍(\bullet)$ and $𝕆𝕍(\bullet,\bullet;\bullet)$. The actions of optics on these two profunctors determine multiple possible insertions of optics and transformations on the context that an optic determines.

The prounit of optics becomes a profunctor, $(𝕆𝕍(\bullet), <)$, with optic evaluation, $$ (<)﹕ 𝕆𝕍\left( \begin{matrix} X \\ X’ \end{matrix} \right) × 𝕆𝕍\left( \begin{matrix} X \\ X’ \end{matrix}; \begin{matrix} Y \\ Y’ \end{matrix} \right) → 𝕆𝕍\left( \begin{matrix} Y \\ Y’ \end{matrix} \right), $$ defined by $f < \langle g_0 \mid g_1 \rangle = g_0 ⨾ (id ⊗ f) ⨾ g_1$.

The protensor of optics becomes a profunctor, $(𝕆𝕍(\bullet,\bullet;\bullet),>_l,>_r,<)$, with the two possible optic insertions and evaluation, $$ (>_l)﹕ 𝕆𝕍\left( \begin{matrix} X \\ X’ \end{matrix}; \begin{matrix} A \\ A’ \end{matrix} \right) × 𝕆𝕍\left( \begin{matrix} A \\ A’ \end{matrix}, \begin{matrix} Y \\ Y’ \end{matrix} ; \begin{matrix} Z \\ Z’ \end{matrix}\right) → 𝕆𝕍\left( \begin{matrix} X \\ X’ \end{matrix}, \begin{matrix} Y \\ Y’ \end{matrix} ; \begin{matrix} Z \\ Z’ \end{matrix}\right), $$ $$ (>_r)﹕ 𝕆𝕍\left( \begin{matrix} Y \\ Y’ \end{matrix}; \begin{matrix} A \\ A’ \end{matrix} \right) × 𝕆𝕍\left( \begin{matrix} X \\ X’ \end{matrix}, \begin{matrix} A \\ A’ \end{matrix} ; \begin{matrix} Z \\ Z’ \end{matrix}\right) → 𝕆𝕍\left( \begin{matrix} X \\ X’ \end{matrix}, \begin{matrix} Y \\ Y’ \end{matrix} ; \begin{matrix} Z \\ Z’ \end{matrix}\right), $$ $$ (<)﹕ 𝕆𝕍\left( \begin{matrix} X \\ X’ \end{matrix}, \begin{matrix} A \\ A’ \end{matrix} ; \begin{matrix} A \\ A’ \end{matrix}\right) × 𝕆𝕍\left( \begin{matrix} A \\ A’ \end{matrix}; \begin{matrix} Z \\ Z’ \end{matrix} \right) → 𝕆𝕍\left( \begin{matrix} X \\ X’ \end{matrix}, \begin{matrix} Y \\ Y’ \end{matrix} ; \begin{matrix} Z \\ Z’ \end{matrix}\right), $$ which are defined by $$\langle g₀ \mid g₁ \rangle \mathbin{>_l}\langle f₀ \mid f₁ \mid f₂ \rangle = \langle f₀ ⨾ (id ⊗ g₀) \mid (id ⊗ g₁) ⨾ f₁ \mid f₂ \rangle,$$ $$\langle h₀ \mid h₁ \rangle \mathbin{>_r}\langle f₀ \mid f₁ \mid f₂ \rangle = \langle f₀ \mid f₁ ⨾ (id ⊗ h₀) \mid (id ⊗ h₁) ⨾ f₂ \rangle,$$ $$ \langle f₀ \mid f₁ \mid f₂ \rangle \mathbin{<} \langle t₀ \mid t₁ \rangle = \langle t₀ ⨾ (id ⊗ f₀) \mid (id ⊗ f₁) \mid (id ⊗ f₂) ⨾ t₁ \rangle.$$

The unitors may be constructed via coend calculus, using the units of the monoidal category. $$ \begin{aligned} & ∫^{\begin{pmatrix} X \\ X’ \end{pmatrix} \in 𝕆𝕍} 𝕆𝕍\left( \begin{matrix} X \\ X’ \end{matrix} \right) × 𝕆𝕍\left( \begin{matrix} X \\ X’ \end{matrix}, \begin{matrix} Y \\ Y’ \end{matrix}; \begin{matrix} Z \\ Z’ \end{matrix} \right) \\ \cong & \quad \mbox{Introducing units by definition of optic.} \\ & ∫^{\begin{pmatrix} X \\ X’ \end{pmatrix} \in 𝕆𝕍} 𝕆𝕍\left( \begin{matrix} X \\ X’ \end{matrix} ; \begin{matrix} I \\ I \end{matrix} \right) × 𝕆𝕍\left( \begin{matrix} X \\ X’ \end{matrix}, \begin{matrix} Y \\ Y’ \end{matrix}; \begin{matrix} Z \\ Z’ \end{matrix} \right) \\ \cong & \quad \mbox{Yoneda reduction.}\\ & 𝕆𝕍\left( \begin{matrix} I \\ I \end{matrix}, \begin{matrix} Y \\ Y’ \end{matrix}; \begin{matrix} Z \\ Z’ \end{matrix} \right) \\ \cong & \quad \mbox{Reducing units by definition of optic.}\\ & 𝕆𝕍\left( \begin{matrix} Y \\ Y’ \end{matrix}; \begin{matrix} Z \\ Z’ \end{matrix} \right) \\ \end{aligned} $$ The associators are finally constructed via coend calculus, by noticing that three-part data accessors have a common representation, independent of that how we get to them. $$ \begin{aligned} & ∫^{\begin{pmatrix} U \\ U’ \end{pmatrix} \in 𝕆𝕍} 𝕆𝕍 \left( \begin{matrix} X \\ X’ \end{matrix}, \begin{matrix} Y \\ Y’ \end{matrix}; \begin{matrix} U \\ U’ \end{matrix} \right) × 𝕆𝕍 \left( \begin{matrix} U \\ U’ \end{matrix}, \begin{matrix} Z \\ Z’ \end{matrix}; \begin{matrix} T \\ T’ \end{matrix} \right) \\ \cong & \quad \mbox{Splitting by definition of optic.} \\ & ∫^{\begin{pmatrix} U \\ U’ \end{pmatrix} \in 𝕆𝕍, C \in 𝕍} 𝕆𝕍 \left( \begin{matrix} X \\ X’ \end{matrix}, \begin{matrix} Y \\ Y’ \end{matrix}; \begin{matrix} U \\ U’ \end{matrix} \right) × 𝕆𝕍 \left( \begin{matrix} U \\ U’ \end{matrix}; \begin{matrix} T \\ C ⊗ Z \end{matrix} \right) × 𝕍 \left( C ⊗ Z’,T' \right) \\ \cong & \quad \mbox{Yoneda reduction.} \\ & ∫^{C \in 𝕍} 𝕆𝕍 \left( \begin{matrix} X \\ X’ \end{matrix}, \begin{matrix} Y \\ Y’ \end{matrix}; \begin{matrix} T \\ C ⊗ Z \end{matrix} \right) × 𝕍 \left( C ⊗ Z’,T' \right) \\ \cong & \quad \mbox{By the definition of protensor.} \\ & ∫^{A, B, C \in 𝕍} 𝕍 (T; A ⊗ X) × 𝕍(A ⊗ X’; B ⊗ Y) × 𝕍(B ⊗ Y’; C ⊗ Z)×𝕍(C ⊗ Z’,T’) \\ \cong & \quad \mbox{By the definition of protensor.} \\ & ∫^{A \in 𝕍} 𝕍 \left( T, A ⊗ X \right) × 𝕆𝕍 \left( \begin{matrix} Y \\ Z \end{matrix}, \begin{matrix} Z \\ Z’ \end{matrix}; \begin{matrix} A ⊗ X’ \\ T’ \end{matrix} \right)\\ \cong & \quad \mbox{Yoneda reduction.} \\ & ∫^{\begin{pmatrix} U \\ U’ \end{pmatrix} \in 𝕆𝕍, A \in 𝕍} 𝕍 \left( T, A ⊗ X \right) × 𝕆𝕍 \left( \begin{matrix} U \\ U’ \end{matrix}; \begin{matrix} A ⊗ X’ \\ T’ \end{matrix} \right) × 𝕆𝕍 \left( \begin{matrix} Y \\ Y’ \end{matrix}, \begin{matrix} Z \\ Z’ \end{matrix}; \begin{matrix} U \\ U’ \end{matrix} \right)\\ \cong & \quad \mbox{Splitting by definition of optic.} \\ & ∫^{\begin{pmatrix} U \\ U’ \end{pmatrix} \in 𝕆𝕍} 𝕆𝕍 \left( \begin{matrix} X \\ X’ \end{matrix}, \begin{matrix} U \\ U’ \end{matrix}; \begin{matrix} T \\ T’ \end{matrix} \right) × 𝕆𝕍 \left( \begin{matrix} Y \\ Y’ \end{matrix}, \begin{matrix} Z \\ Z’ \end{matrix}; \begin{matrix} U \\ U’ \end{matrix} \right). \end{aligned} $$