Span(Graph), a Canonical Feedback Algebra of Open Transition Systems (Di Lavore et al)
- Article: pdf.
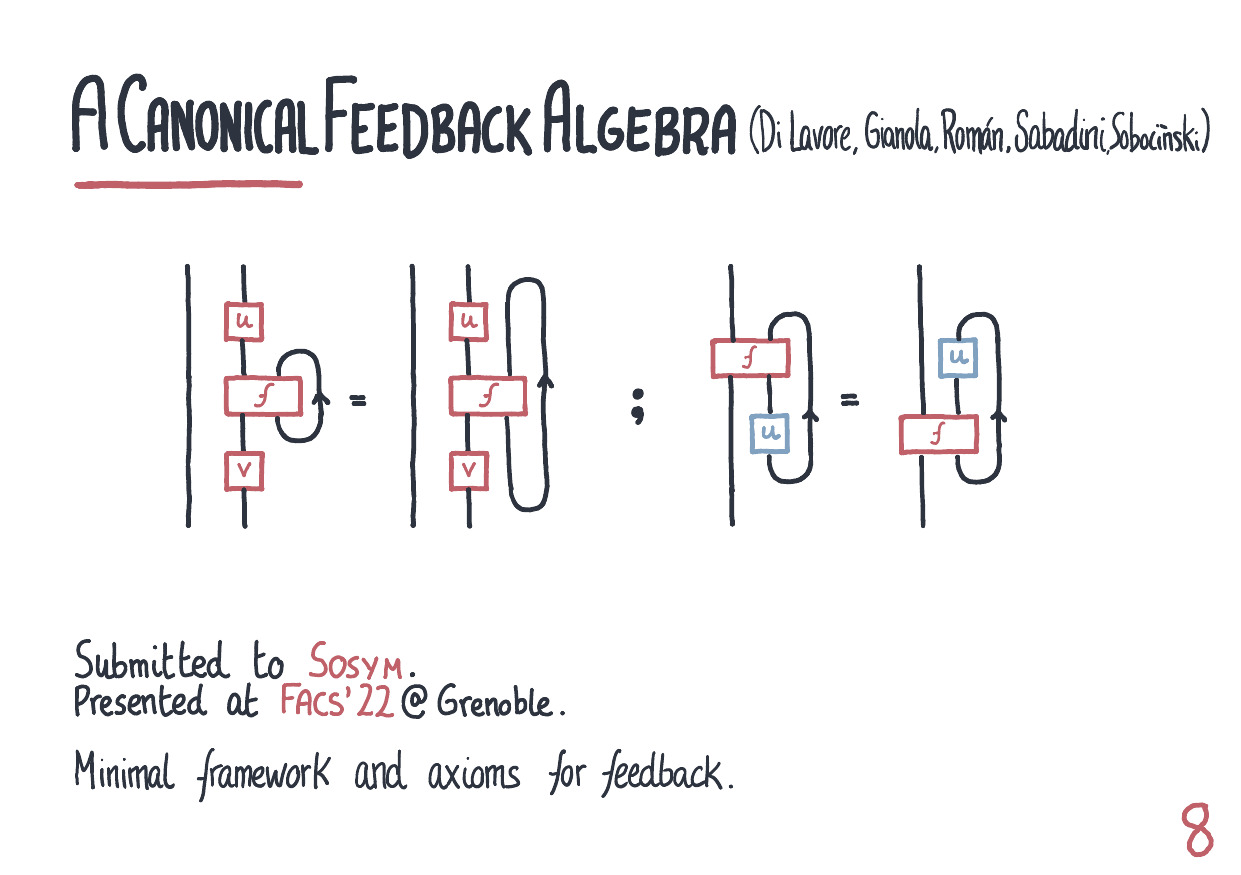
Abstract. We show that Span(Graph), an algebra for open transition systems introduced by Katis, Sabadini and Walters, satisfies a universal property. By itself, this is a justification of the canonicity of this model of concurrency. However, the universal property is itself of interest, being a formal demonstration of the relationship between feedback and state. Indeed, feedback categories, also originally proposed by Katis, Sabadini and Walters, are a weakening of traced monoidal categories, with various applications in computer science. A state bootstrapping technique, which has appeared in several different contexts, yields free such categories. We show that Span(Graph) arises in this way, being the free feedback category over Span(Set). Given that the latter can be seen as an algebra of predicates, the algebra of open transition systems thus arises - roughly speaking - as the result of bootstrapping state to that algebra. Finally, we generalize feedback categories endowing state spaces with extra structure: this extends the framework from mere transition systems to automata with initial and final states.