The Produoidal Algebra of Process Decomposition (Earnshaw, Hefford, Román, 2023)

Last updated Unknown

• Article: pdf.
• Slides: Ottawa Logic Seminar.
• Slides: MFPS 2023.
• Extended Abstract: Contouring Prostar Autonomous Categories.

Abstract. We introduce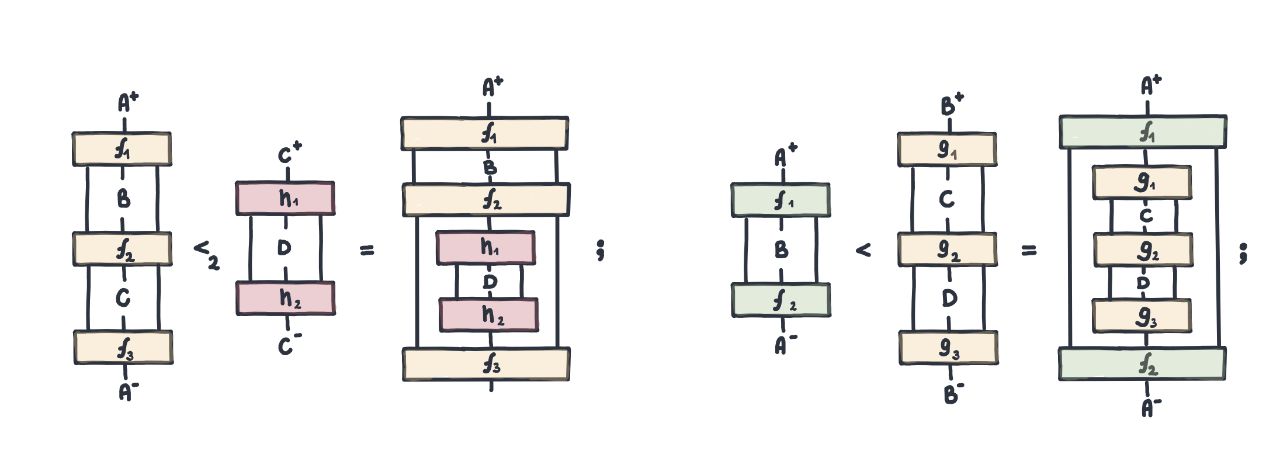 the normal produoidal category of monoidal contexts over an arbitrary monoidal category. In the same sense that a monoidal morphism represents a process, a monoidal context represents an incomplete process: a piece of a decomposition, possibly containing missing parts. We characterize monoidal contexts in terms of universal properties. In particular, symmetric monoidal contexts coincide with monoidal lenses, endowing them with a novel universal property. We apply this algebraic structure to the analysis of multi-party interaction protocols in arbitrary theories of processes.