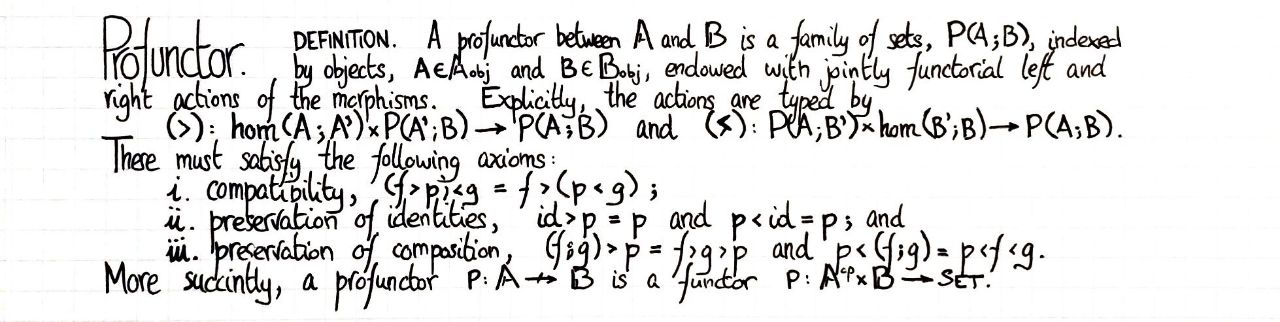
Profunctors.
Profunctors form a bicategory: hom is the identity profunctor, and profunctor composition is associative.
Promonads.
- motivation for promonads
- promonad, a monoid in the bicategory of profunctors
- promonad homomorphism, or natural transformation
- Kleisli category of a promonad
- Promonads are id-on-objects functors
- Central product of promonads
- Pure tensor of promonads
- Funny tensor of promonads
- distributive law of promonads
- distributive law of strong promonads
- promodule
Promonoidal categories.
Strong profunctors, with a bit of promonoidals.
- Strong profunctor
- Bimodular profunctor
- pro or not, strong or not
- Strong monad
- Strong promonad
- Prostrong monad
- Prostrong promonad
Monoidal profunctors.
- monoidal profunctor
- monoidal promonad
- Map pseudomonoid
- Lax twisted arrow bicategory
- Mates correspondence
- Convolution and coconvolution
- Duoidal Tambara
- produoidal normalization
- Raudsilla Seminar, November 2022
Monoidal bicategory of profunctors.
- monoidal bicategory of profunctors
- Reading an example on the monoidal bicategory of profunctors
- Open diagram
- open diagrams are pointed profunctors
Profunctors with structure.
- multivariable adjunction
- Pointed profunctor
- Lack coherence theorem
- Composition along a channel
- Reversors in profunctors
Tags: category theory.