Lax twisted arrow bicategory
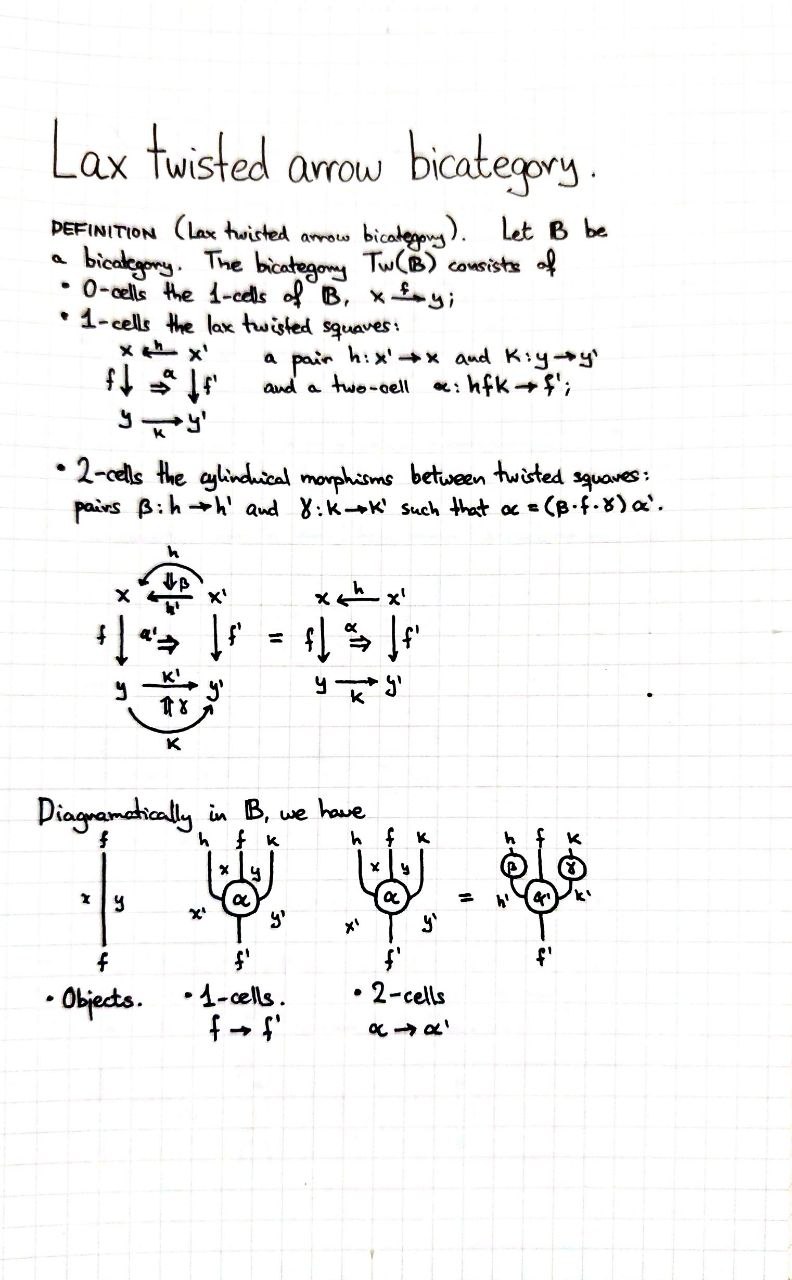
Definition. Let $(ℂ,⊗,I)$ be a bicategory. I call the lax-twisted arrow bicategory $\mathsf{Tw}(ℂ)$ the monoidal bicategory where
- 0-cells are arrows $f \colon A → B$ in $ℂ$;
- 1-cells are lax-twisted squares;
- the monoidal unit is $\mathrm{id} \colon I → I$;
- the monoidal tensor is the tensor of arrows;
- and 2-cells are cylindrical fillings.
Pseudomonoids in the lax-twisted arrow bicategory are
Twisted arrow pseudomonoids.
Tags: Arrow category, Monoids on the arrow category, bicategory.